When two bodies, a heavy one and a light one, are acted upon by the same force for the same time, the light body attains a higher velocity (or higher speed) than the heavy one. But the momentum gained by both the bodies is the same. The link between force and momentum is expressed in Newton’s second law of motion.
According to Newton’s second law of motion : The rate of change of momentum of a body is directly proportional to the applied force, and takes place in the direction in which the force acts. The rate of change of momentum of a body can be obtained by dividing the ‘Change in momentum’ by Time taken’ for change. So, Newton’s second law of motion can be expressed as :
Force ∝ change in momentum / time taken
Consider a body of mass m having an initial velocity u. The initial momentum of this body will be mu. Suppose a force F acts on this body for time t and causes the final velocity to become v. The final momentum of this body will be mv. Now, the change in momentum of this body is my – mu and the time taken for this change is t. So, according to Newton’s second law of motion :
F ∝ mv – mu/t
Or F ∝ m( v – u )/t
But v-u / t represents change in velocity with time which is known as acceleration ‘a’. So, by writing ‘a ‘ in place of v- u / t in the above relation, we get:
F ∝ m × a
Thus, the force acting on a body is directly proportional to the product of ‘mass’ of the body and acceleration’ produced in the body by the action of the force, and it acts in the direction of acceleration. This is another definition of Newton’s second law of motion.
The relation F ∝ m × a can be turned into an equation by putting in a constant k.
Thus, F = k × m × a ( where k is a constant)
The value of constant k in SI units is 1, so the above equation becomes:
F = m × a
Or force = mass × acceleration
Thus, Newton’s second law of motion gives us a relationship between ‘force’ and ‘acceleration’. When a force acts on a body, it produces acceleration in the body, the acceleration produced may be positive or negative. Newton’s second law of motion also gives us a method of measuring the force in terms of mass and acceleration. The force acting on a body can be calculated by using the formula : F = m × a. We can also write the equation F = m x a as:
a = F/m
It is obvious from the above relation that : The acceleration produced in a body is directly proportional to the force acting on it and inversely proportional to the mass of the body. Since the acceleration produced is inversely proportional to the mass of a body, therefore, if the mass of a body is doubled, its acceleration will be halved. And if the mass is halved then acceleration will get doubled (provided the force remains the same). Moreover, since the acceleration produced is inversely proportional to the mass of the body, it means that it will be easier to move light bodies (having less mass) than heavy bodies (having large mass).
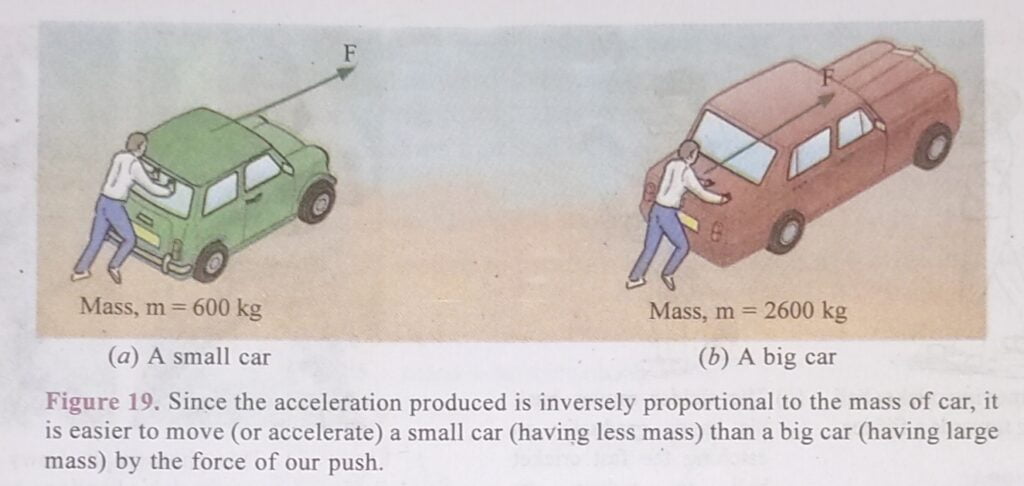
The SI unit of force is newton which is denoted by N. A newton is that force which when acting on a body of mass 1 kg produces an acceleration of 1 m/s² in it. We have just seen that :
F = m × a
putting m = 1kg and a=1 ms/s², F become 1 newton
so, 1 newton = 1 kg × 1m/s²
In order to get an idea of 1 newton force, we should hold a weight of 100 grams on our outstretched palm. The force exerted by 100 gram weight on our palm is approximately equal to 1 newton.
The first law of motion discussed earlier is, in fact, a special case of the second law, because when the applied force F is zero, then the acceleration ‘a’ is also zero and the body remains in its state of rest or of uniform motion. It is obvious that Newton’s second law gives us a relationship between the force applied to a body and the acceleration produced .in the body. The formula F = m x a should be memorized because it will be used to solve numerical problems.
It should be noted that just as a minus sign for acceleration shows that the acceleration is acting in a direction opposite to the motion of the body, in the same way, if a minus sign comes with the force, it will indicate that the force is acting in a direction opposite to that in which the body is moving (just as the force of friction acts in a direction opposite to that of the moving body).
Applications of Newton’s Second Law of Motion
Some of the observations of our daily life can be explained on the basis of Newton’s second law of motion. In all these cases some technique or arrangement is used to reduce the momentum of a fast moving body more gently (by allowing more time to stop it), so that injury can be prevented or reduced. Here are some examples.
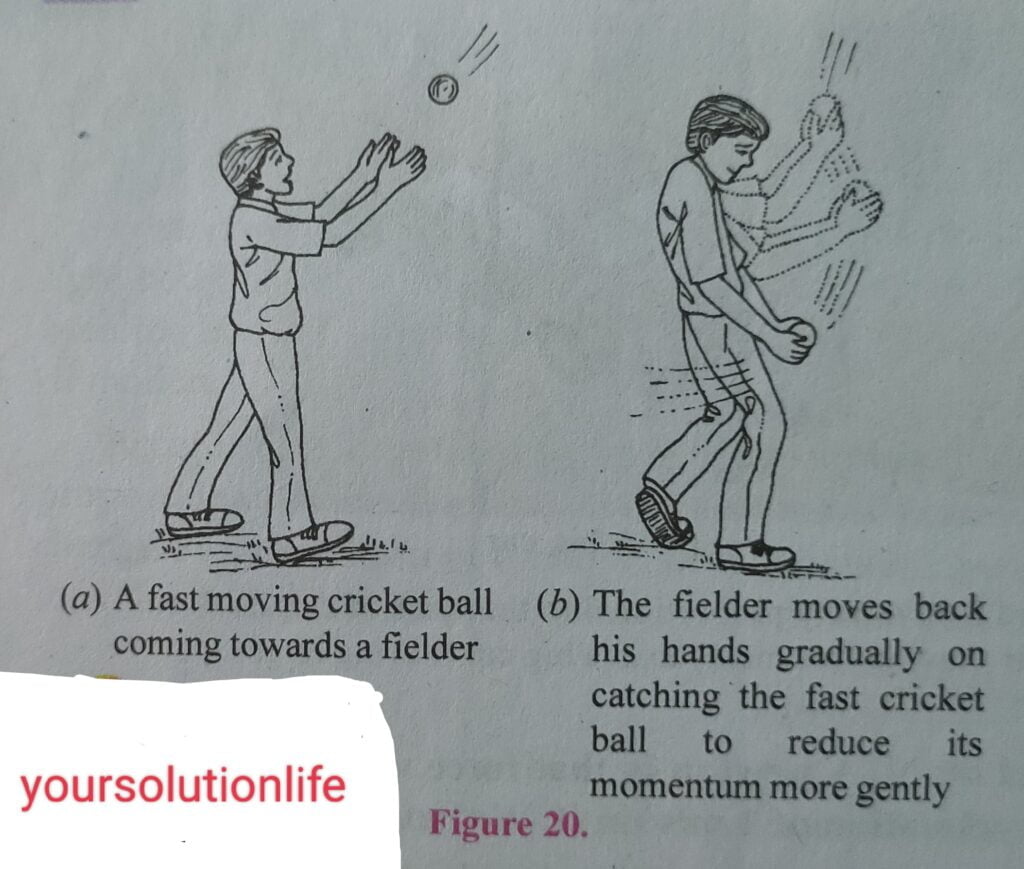
1. Catching a Cricket Ball
A cricket player (or fielder) moves his hands backwards on catching a fast cricket ball. This is done to prevent injury to the hands. We can explain it as follows : A fast moving cricket ball has a large momentum. In stopping (or catching) this cricket ball, its momentum has to be reduced to zero. Now, when a cricket player moves back his hands on catching the fast ball, then the time taken to reduce the momentum of ball to zero is increased (see Figure 20). Due to more time taken to stop the ball, the rate of change of momentum of ball is decreased and hence a small force is exerted on the hands of player. So, the hands of player do not get hurt.
If, however, a cricket player stops a fast moving ball suddenly (keeping his hands stationary), then the large momentum of the ball will be reduced to zero in a very short time. Due to this, the rate of change of momentum of cricket ball will be very large and hence it will exert a large force on player’s hands. The player’s hands will get hurt.

2. The Case of a High Jumper
During athletics meet, a high jumping athlete is provided either a cushion or a heap of sand on die ground to fall upon. This is done to prevent injury to the athlete when he falls down after making a nigh jump. We can explain it as follows : When the high jumper falls on a soft landing site (such as a cushion or a heap of sand), then the jumper takes a longer time to come to a stop. The rate of change of momentum of athlete is less due to which a smaller stopping force acts on the athlete. And the athlete does not get hurt. Thus, the cushion or sand, being soft, reduces the athlete’s momentum more gently. If, however, a high jumping athlete falls from a height on to hard ground, then his momentum will be reduced to zero in a very short time. The rate of change of momentum will be large due to which a large opposing force will act on the athlete. This can cause serious injuries to the athlete.

3. The Use of Seat Belts in Car
These days all the cars are provided with seat belts for passengers to prevent injuries in case of an accident. In a car accident, a fast running car stops suddenly. Due to this the car’s large momentum is reduced to zero in a very short time. The slightly stretchable seat belts worn by the passengers of the car increase the time taken by the passengers to fall forward. Due to longer time, the rate of change of momentum of passengers is reduced and hence less stopping force acts on them. So, the passengers may either not get injured at all or may get less injuries. It is obvious that seat belts reduce the passengers’ momentum more gently and hence prevent injuries .
We will now solve some problems based on Newton’s second law of motion.
Sample Problem 1. What force would be needed to produce an acceleration of 4 m/s2 in a ball of mass 6 kg ?
Solution. The force needed is to be calculated by using the relation :
Force = mass x acceleration
or F = m x a
Here, Force, F = ? (To be calculated)
Mass, m = 6 kg
And Acceleration, a = 4m/s²
Now, putting these values of m and a in the above equation, we get :
F = 6 x 4
Force, F = 24N
Thus, the force needed is of 24 newton.

