The three equations of motion : v = u + at ; s = ut +1/2 at² and v² = u² +2as can be derived with the help of graphs as described below.
1. To Derive v = u + at by Graphical Method
Consider the velocity-time graph of a body shown in Figure 43. The body has an initial velocity u at point A and then its velocity changes at a uniform rate from A to B in time t. In other words, there is a uniform acceleration a from A to B, and after time t its final velocity becomes v which is equal to BC in the graph (see Figure 43). The time t is represented by OC. To complete the figure, we draw the perpendicular CB from point C, and draw AD parallel to OC. BE is the perpendicular from point B to OE.
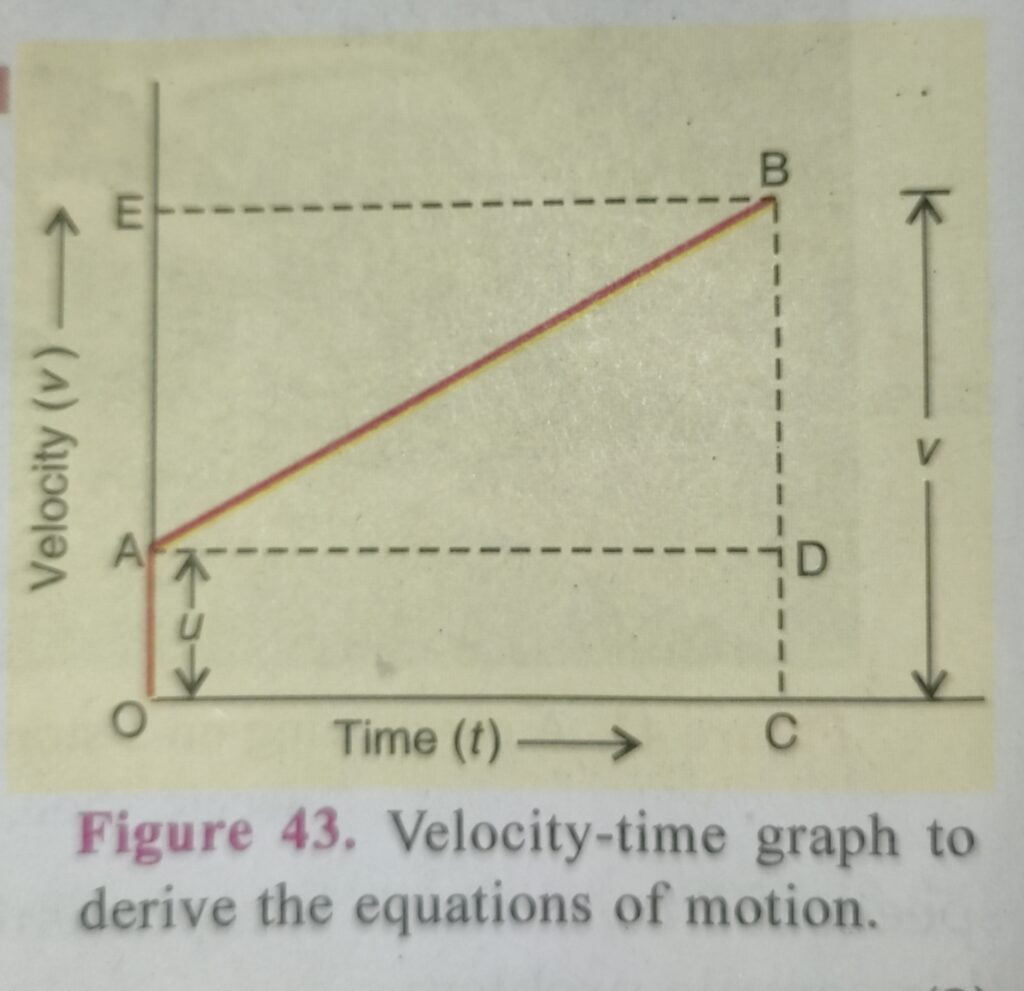
Now, Initial velocity of the body, u = OA. …( 1 )
And, Final velocity of the body, v = BC .. ….( 2 )
But from the graph BC = BD + DC
Therefore,. v = BD + DC … ( 3 )
Again DC = OA
So, v = BD + OA
Now, From equation (1), OA = u.
So, V = BD + u ….( 4 )
We should find out the value of BD now. We know that the slope of a velocity-time graph is equal to acceleration, a.
Thus, Acceleration, a = slope of line AB (see Figure 43)
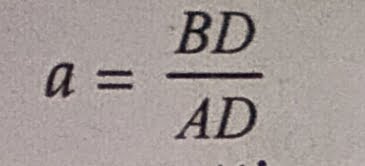
But AD = OC = t (see Figure 43), so putting t in place of AD in the above relation, we get :

Now, putting this value of BD in equation (4) we get :
v = u + at
This equation can be rearranged to give :
v = u + at
And this is the first equation of motion. It has been derived here by the graphical method.
2. To Derive s = ut + 1/2at² by Graphical Method
Suppose the body travels a distance s in time t. In Figure 43, the distance travelled by the body is given by the area of the space between the velocity-time graph AB and the time axis OC, which is equal to the area of the figure OABC. Thus :
Distance travelled = Area of figure OABC
= Area of rectangle OADC + Area of triangle ABD
We will now find out the area of the rectangle OADC and the area of the triangle ABD.
(i) Area of rectangle OADC = OA x OC (see Figure 43)
= u x t
= ut
(ii) Area of triangle ABD =1/2 x Area of rectangle AEBD
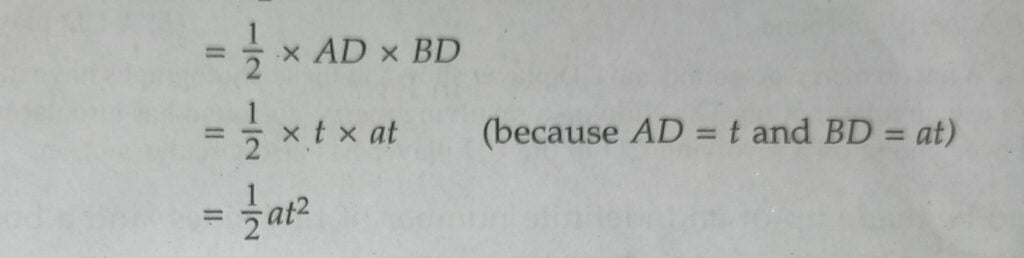
So, Distance travelled, s = Area of rectangle OADC + Area of triangle ABD
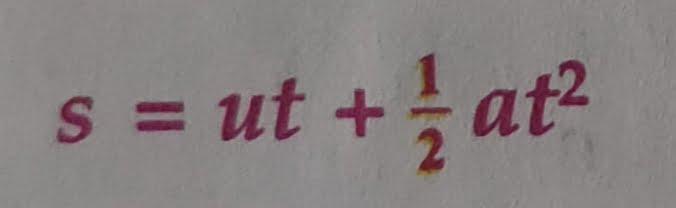
thus is the second equation of motion. It has been derived here by the graphical method.
3. To Derive v² = u² + 2as by Graphical Method
We have just seen that the distance travelled s by a body in time t is given by the area of the figure OABC which is a trapezium (see Figure 43). In other words,
Distance travelled, s = Area of trapezium OABC
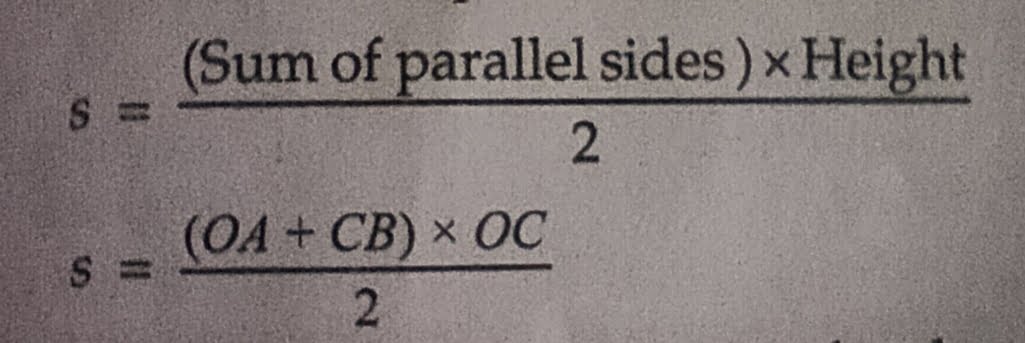
Now, OA + CB = u + v and OC = t. Putting these values in the above relation, we get:
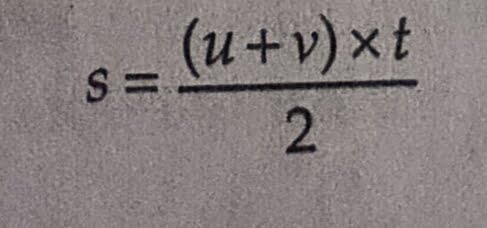
We now want to eliminate t from the above equation. This can be done by obtaining the value of t from the first equation of motion.
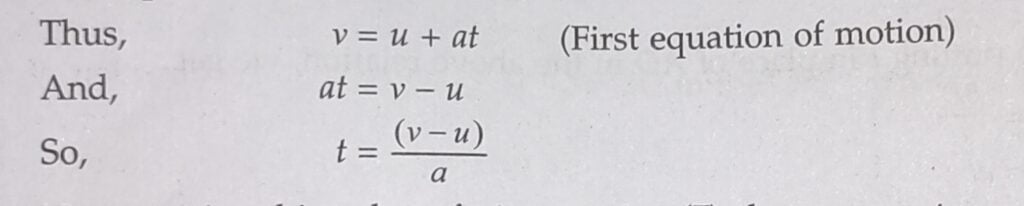
Now, putting this value of t in equation (7) above, we get:
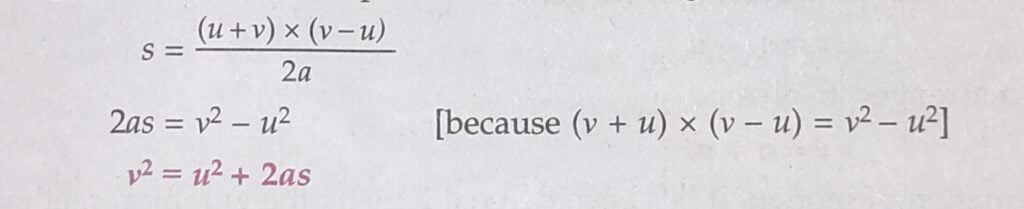
This is the third equation of motion. It has been derived by the graphical method.

